Contoh Soal Gelombang Berjalan Beserta Pembahasannya – Gelombang berjalan adalah gelombang yang merambat dengan amplitudo tetap. Secara umum, persamaan simpangan di suatu titik sembarang pada tali (misalnya titik P), yang berjarak x dari titik asal getaran adalah sebagai berikut :
$$y=±A\sin2π(\frac{t}{T}∓\frac{x}{λ})$$
Dengan fase gelombang : $\phi = \frac{t}{T}∓\frac{x}{\lambda}$, dan 2πφ disebut sebagai sudut fase.
Tanda negatif dalam sinus diberikan untuk gelombang berjalan yang merambat ke kanan, sedangkan tanda positif diberikan untuk gelombang berjalan yang merambat ke kiri. Tanda positif pada A (amplitudo) diberikan jika titik asal getaran O untuk pertama kalinya bergerak ke atas, sedangkan tanda negatif pada A diberikan jika titik asal getaran O untuk pertama kalinya bergerak ke bawah. Untuk titik asal getaran berlaku x = 0. Persamaan simpangan dapat ditulis dalam bentuk :
$$y=±A\sin(\omega t ∓kx )$$
Rumus kecepatan partikel di titik P :
$$v=ωA\cos(ωt–kx) $$
Rumus percepatan partikel di titik P
$$a=−ω^2A\sin(ωt–kx)=−ω^2y$$
Sudut Fase
Sudut fase adalah besar sudut dalam fungsi sinus (dinyatakan dalam radian)
$$θ=2π\left( \frac{t}{T}–\frac{x}{λ} \right)$$
Beda Fase
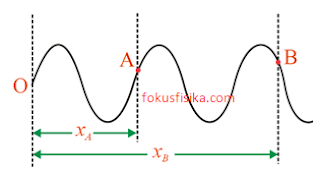
Beda fase antara titik A dan B adalah
$$Δφ=\frac{−(x_B–x_A)}{λ}=\frac{−Δx}{λ} $$
Tanda negatif menunjukkan bahwa untuk gelombang yang merambat ke sumbu x positif, partikel yang terletak di depan (sebelah kanan) mengalami keterlambatan fase terhadap partikel di belakangnya (sebelah kiri).
Contoh Soal dan Pembahasan Gelombang Berjalan
Contoh Soal 1
Besaran yang dimiliki baik oleh getaran maupun gelombang adalah :
1. panjang gelombang
2. amplitudo
3. cepat rambat
4. frekuensi
Pernyataan yang benar adalah ….
A. 1, 2, dan 3
B. 1 dan 3
C. 2 dan 4
D. 4 saja
E. semua benar
Pembahasan :
Besaran yang dimiliki oleh getaran maupun gelombang yaitu amplitudo dan frekuensi
Jawaban : C
Contoh Soal 2
Sebuah perahu kecil bergerak naik turun sebanyak sepuluh kali dalam satu menit pada gelombang air laut. Jarak puncak gelombang yang berdekatan adalah 24 m. Kecepatan gelombang air laut itu besarnya ….
A. 1 m/s
B. 4 m/s
C. 8 m/s
D. 12 m/s
E. 15 m/s
Pembahasan :
$$ f =\frac{n}{t} = \frac{10}{60} = 0,16 \quad \textrm{Hz} $$
$$v=λ\cdot f=24\cdot 0,16=4\quad \textrm{m/s} $$
Jawaban : B
Contoh Soal 3
Berapa kalikah dalam satu menit sebuah perahu akan bergerak nait-turun oleh gelombang lautan, yang panjang gelombangnya 40 m dan laju perambatannya 5 m/s?
A. 2,5 kali
B. 5,0 kali
C. 7,5 kali
D. 10,0 kali
E. 12,5 kali
Pembahasan :
$$
\begin{align*}
v &= \lambda \cdot f \\
5 &= 40\cdot f \\
f &= \frac{5}{40} \\
&= 0,125 \quad \textrm{Hz}
\end{align*}
$$
Banyaknya naik turun perahu dalam satu menit :
$$
\begin{align*}
f &= \frac{n}{t} \\
0,125 &= \frac{n}{60} \\
n &= 7,5 \quad \textrm{kali}
\end{align*}
$$
Jawaban : C
Contoh Soal 4
Berikut ini adalah persamaan simpangan gelombang berjalan y = 10 sin π(0,4t – 10,5x). Periode gelombangnya adalah ….
A. 4 s
B. 5 s
C. 6 s
D. 7 s
E. 8 s
Pembahasan :
$y = 10 \sin π(0,4t – 10,5x) = 10 \sin (0,4πt – 10,5πx)$
$$
\begin{align*}
\omega &= \frac{2\pi}{T} \\
0,4\pi &= \frac{2\pi}{T}\\
T &= 5 \quad \textrm{s}
\end{align*}
$$
Jawaban : B
Contoh Soal 5
Suatu gelombang air laut menyebabkan permukaan air naik turun dengan periode 3 s. Jika jarak antara dua puncak gelombang 5 m, gelombang akan mencapai jarak 10 m dalam waktu ….
A. 1 s
B. 2 s
C. 3 s
D. 6 s
E. 10 s
Pembahasan :
$$
\begin{align*}
v &=\frac{\lambda}{T} \\
v &=\frac{5}{3} \quad \textrm{s}
\end{align*}
$$
Gelombang mencapai jarak 10 m dalam waktu :
$$
\begin{align*}
v &=\frac{x}{t} \\
\frac{5}{3} &=\frac{10}{t} \\
5t &= 30 \\
t &= 6 \quad \textrm{s}
\end{align*}
$$
Jawaban : D
Contoh Soal 6
Suatu gelombang berjalan memenuhi persamaan y = 0,2 sin 2π (60t – 2x) dengan y dan x dalam meter dan t dalam sekon. Cepat rambat gelombang tersebut adalah ….
A. 15 m/s
B. 25 m/s
C. 30 m/s
D. 45 m/s
E. 60 m/s
Pembahasan :
$y=0,2\sin 2\pi (60t – 2x) = 0,2 \sin (120\pi t – 4\pi x)$
Dari persamaan di atas diperoleh frekuensi :
$$
\begin{align*}
\omega &=2\pi f \\
120\pi &=2\pi f \\
f &= 60 \quad \textrm{Hz}
\end{align*}
$$
Dan panjang gelombangnya :
$$
\begin{align*}
\frac{2\pi}{\lambda} &=4\pi \\
\lambda &= 0,5 \quad \textrm{m}
\end{align*}
$$
Sehingga cepat rambat gelombangnya :
$$
\begin{align*}
v &=\lambda \cdot f \\
v &=0,5 \cdot 60 \\
v &= 30 \quad \textrm{m/s}
\end{align*}
$$
Jawaban : C
Contoh Soal 7
Suatu gelombang merambat dengan persamaan y = 4 sin π(3t – 0,2x). Jika y dan x dalam m dan t dalam s, besar frekuensi dan panjang gelombang masing-masing adalah ….
A. 0,6 Hz dan 0,1 m
B. 1,5 Hz dan 10 m
C. 2 Hz dan 0,4 m
D. 3 Hz dan 20 m
E. 3 Hz dan 30 m
Pembahasan :
$y=4 \sin \pi (3t-0,2x) =4 \sin (3πt-0,2πx) $
Besar frekuensi :
$$
\begin{align*}
\omega &=2\pi \cdot f \\
3\pi &=2\pi \cdot f \\
f &= \frac{3}{2} \\
& = 1,5 \quad \textrm{Hz}
\end{align*}
$$
Besar panjang gelombang :
$$
\begin{align*}
k &= \frac{2\pi}{\lambda} \\
0,2\pi &=\frac{2\pi}{\lambda} \\
\lambda &= 10 \quad \textrm{m}
\end{align*}
$$
Jawaban : B
Contoh Soal 8. Soal SBMPTN 2016/SAINTEK/237/30
Suatu gelombang sinusoidal bergerak dalam arah x-positif, mempunyai amplitudo 15,0 cm, panjang gelombang 40,0 cm dan frekuensi 8,0 Hz. Jika posisi vertikal dari elemen medium pada t = 0 dan x = 0 adalah 15,0 cm, maka bentuk umum fungsi gelombangnya adalah ….
A. $y=(15,0 \quad \textrm{cm}) \sin (0,157x+50,3t-\frac{\pi}{2})$
B. $y=(15,0 \quad \textrm{cm}) \cos (0,157x-50,3t-\frac{\pi}{4})$
C. $y=(15,0 \quad \textrm{cm}) \sin (0,157x+50,3t+\frac{\pi}{2})$
D. $y=(15,0 \quad \textrm{cm}) \cos (0,157x-50,3t)$
E. $y=(15,0 \quad \textrm{cm}) \cos (0,157x+50,3t)$
Pembahasan :
Fungsi umum gelombang : $ y = A\sin (kx-\omega t + \theta _o)$
Selanjutnya kita tentukan koefisien-koefisiennya :
$$
\begin{align*}
k &= \frac{2\pi}{\lambda} \\
&= \frac{2\pi}{40} \\
&= 0,157
\end{align*}
$$
$$
\begin{align*}
\omega &= 2\pi f \\
&= 2\pi \cdot 8 \\
&= 50,3
\end{align*}
$$
Jadi : $y=(15,0 \quad \textrm{cm}) \sin (0,157x-50,3t+\theta _o )$
Saat t = 0 dan x = 0 –> y = 15,0 sehingga :
$$
\begin{align*}
y &= 15 \sin (0,157x-50,3t+\theta _o) \\
15&= 15 \sin (0-0+\theta _o) \\
1&= \sin \theta _o \\
\theta _o &= \frac{\pi}{2}
\end{align*}
$$
Ingat bahwa : $\sin (\frac{\pi}{2} + \alpha) = \cos \alpha$
Jadi :
$$
\begin{align*}
y &= 15 \sin (0,157x-50,3t+\frac{\pi}{2}) \\
y&= 15 \cos (0,157x-50,3t)
\end{align*}
$$
Jawaban : D
Contoh Soal 9.
Perhatikan skema gelombang berikut.

Jika gelombang P — Q terjadi selama 0,5 s; frekuensi dan cepat rambat gelombang berturut-turut adalah ….
A. 2,5 Hz dan 4 m/s
B. 2,5 Hz dan 8 m/s
C. 5 Hz dan 4 m/s
D. 5 Hz dan 8 m/s
E. 6 Hz dan 9,6 m/s
Pembahasan :
gelombang P — Q terjadi selama 0,5 s, maka :
$$
\begin{align*}
3T &= 0,5 \\
T &= \frac{\frac{1}{2}}{3} \\
T &= \frac{1}{6} \quad\textrm{s}
\end{align*}
$$
Frekuensi gelombang :
$$
\begin{align*}
f &=\frac{1}{T} \\
f &= \frac{1}{\frac{1}{6}} \\
f &= 6 \quad\textrm{Hz}
\end{align*}
$$
Panjang gelombang :
$$
\begin{align*}
2,5\lambda &=4 \\
\lambda &= 1,6 \quad\textrm{m}
\end{align*}
$$
Cepat rambat gelombang :
$$
\begin{align*}
v &=\lambda f \\
&= 1,6\cdot 6 \\
&=9,6 \quad\textrm{m/s}
\end{align*}
$$
Jawaban : D