Artikel ini membahas soal vektor untuk pelajaran fisika. Artikel berisi soal vektor fisika lengkap beserta pembahasan dan penjelasan secara terperinci.
Soal Vektor Fisika No. 1
Perhatikan kelima diagram vektor berikut.
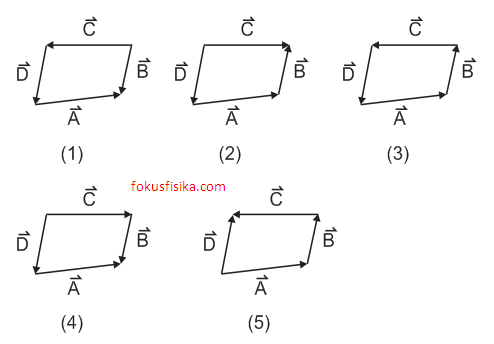
Gambar yang menunjukkan $\vec{A} +\vec{B}+\vec{C}+\vec{D} = 0$ adalah nomor ….
A. (5)
B. (4)
C. (3)
D. (2)
E. (1)
Pembahasan soal vektor fisika no. 1:
Gambar (1)
$$
\begin{align*}
\vec{A} &= -\vec{D}-\vec{C}+\vec{B} \\
\vec{A}-\vec{B}+\vec{C}+\vec{D} &= 0
\end{align*}
$$
Gambar (2)
$$
\begin{align*}
\vec{A} &= -\vec{D}+\vec{C}-\vec{B} \\
\vec{A}+\vec{B}-\vec{C}+\vec{D} &= 0
\end{align*}
$$
Gambar (3)
$$
\begin{align*}
\vec{A} &= -\vec{D}-\vec{C}-\vec{B} \\
\vec{A}+\vec{B}+\vec{C}+\vec{D} &= 0
\end{align*}
$$
Gambar (4)
$$
\begin{align*}
\vec{A} &= -\vec{D}+\vec{C}+\vec{B} \\
\vec{A}-\vec{B}-\vec{C}+\vec{D} &= 0
\end{align*}
$$
Gambar (5)
$$
\begin{align*}
\vec{A} &= +\vec{D}-\vec{C}-\vec{B} \\
\vec{A}+\vec{B}+\vec{C}-\vec{D} &= 0
\end{align*}
$$
Jawaban soal vektor fisika no. 1 : C
Soal Vektor No. 2
Sebuah vektor 8 N diuraikan menjadi dua vektor yang saling tegak lurus dan salah satunya membentuk sudut 60⁰ terhadap vektor tersebut. Besar komponen masing-masing vektor adalah ….
A. 4 N dan $4\sqrt{2}$ N
B. 4 N dan $4\sqrt{3}$ N
C. 4 N dan 8 N
D. 4 N dan $8\sqrt{2}$ N
E. $4\sqrt{2}$ N dan 8 N
Pembahasan soal vektor no. 2 :
Misalkan vektor $\vec{A}$=8 N, kemudian vektor $\vec{A}$ diuraikan terhadap sumbu x dan y, sehingga menjadi Ax dan Ay . Ax membentuk sudut 60o terhadap vektor $\vec{A}$ , sehingga :
$A_x = A\cos 60^o = 8 \cdot \frac{1}{2} = 4 \quad \textrm{N}$
$A_y = A\sin 60^o = 8 \cdot \frac{1}{2}\sqrt{3} = 4\sqrt{3} \quad \textrm{N}$
Jawaban soal vektor no. 2 : B
Soal Vektor No. 3
Vektor $\left|\vec{A} \right|$= 20 satuan, $\left|\vec{B} \right|$ = 21 satuan, sedangkan $\left|\vec{A}+\vec{B} \right|$= 29 satuan. Besar sudut apit kedua vektor tersebut adalah ….
A. 30o
B. 45o
C. 60o
D. 75o
E. 90o
Pembahasan soal vektor no. 3 :
$$
\begin{align*}
\left|\vec{A}+\vec{B} \right| &= 29 \\
\sqrt{A^2 +B^2 +2AB\cos \theta } &= 29 \\
\sqrt{20^2 +21^2 +2\cdot 20\cdot 21 \cos \theta } &= 29 \\
\sqrt{400 +441 +840 \cos \theta } &= 29 \\
400 +441 +840 \cos \theta &= 841 \\
841 + 840 \cos \theta &= 841 \\
840 \cos \theta &= 0 \\
\cos \theta &= 0 \\
\theta &= 90^o
\end{align*}
$$
Jawaban soal vektor no. 3 : E
Soal Vektor No. 4
Seorang anak berlari lurus 7 m ke barat, kemudian belok ke selatan sejauh 8 m, dan berbelok lagi ke timur sejauh 13 m. Perpindahan yang dilakukan oleh anak tersebut dari posisi awal adalah ….
A. 26 m arah timur
B. 14 m arah tenggara
C. 10 m arah barat laut
D. 10 m arah tenggara
E. 8 m arah tenggara
Pembahasan soal vektor no. 4:
Perhatikan gambar di bawah ini:
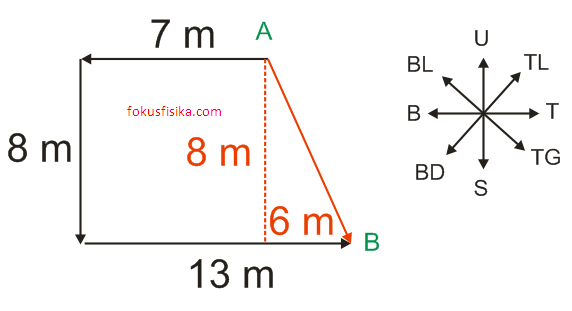
Besar perpindahan benda :
$AB = \sqrt{8^2 + 6^2} = \sqrt{64+36} = \sqrt{100} = 10 \quad \textrm{m}$
Jawaban : D
Soal Vektor No. 5
Terdapat tiga vektor setitik tangkap seperti gambar berikut.

$\left|\vec{A} \right| = \left|\vec{B} \right| = \frac{35}{3}\sqrt{3}$
$\left|\vec{C} \right| = 12$ m
Besar resultan tiga vektor tersebut adalah ….
A. 37 m
B. 35 m
C. 17,5
D. 12 m
E. 6 m
Pembahasan soal vektor No. 5 :
Komponen vektor $\left|\vec{A} \right|$ :
$A_x = A\cos 60 = \frac{35}{3}\sqrt{3} \cdot \frac{1}{2} = \frac{35}{6}\sqrt{3}$
$A_y = A\sin 60 = \frac{35}{3}\sqrt{3} \cdot \frac{1}{2}\sqrt{3} = \frac{35}{2}$
Komponen vektor $\left|\vec{B} \right|$ :
$B_x = -B\cos 60 = -\frac{35}{3}\sqrt{3} \cdot \frac{1}{2} = -\frac{35}{6}\sqrt{3}$
$B_y = B\sin 60 = \frac{35}{3}\sqrt{3} \cdot \frac{1}{2}\sqrt{3} = \frac{35}{2}$
Komponen vektor $\left|\vec{C} \right|$ :
Cx = 12 m
Cy = 0 m
$\Sigma R_x = A_x + B_x + C_x = \frac{35}{6}\sqrt{3} -\frac{35}{6}\sqrt{3} + 12 = 12$ m
$\Sigma R_y = A_y + B_y + C_y = \frac{35}{2}+\frac{35}{2} + 0 = 35$ m
Resultan tiga vektor di atas :
$$
\begin{align*}
\left|\vec{R} \right| &= \sqrt{(\Sigma R_x)^2+(\Sigma R_y)^2} \\
&= \sqrt{(12)^2+(35)^2} \\
&= \sqrt{144+1225} \\
&= \sqrt{1369} \\
&=37 \quad \textrm{m}
\end{align*}
$$
Jawaban soal vektor no. 5 : A
Soal Vektor No. 7
Tiga vektor $\vec{F_1}$ dan $\vec{F_3}$ yang besarnya sama 10 N serta \vec{F_2} besarnya 6 N, berada pada titik tangkap seperti pada gambar berikut.
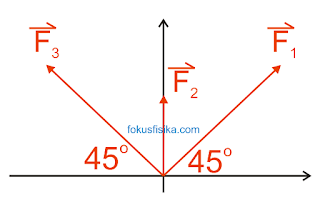
Besar dan arah vektor resultan tersebut ….
A. 6 N searah $\vec{F_1}$
B. 10 N searah $\vec{F_1}$
C. 20 N searah $\vec{F_2}$
D. $\left(10\sqrt{2}+6 \right)$ N searah $\vec{F_2}$
E. $\left(10\sqrt{3}+6 \right)$ N searah $\vec{F_2}$
Pembahasan soal vektor no. 7 :
Komponen vektor $\vec{F_1}$ :
$F_{1x}=F_1\cos 45 = 10\cdot \frac{1}{2}\sqrt{2} = 5\sqrt{2}$ N
$F_{1y}=F_1\sin 45 = 10\cdot \frac{1}{2}\sqrt{2} = 5\sqrt{2}$ N
Komponen vektor $\vec{F_2}$ :
$F_{2x}=F_2\cos 90 = 6\cdot 0 = 0$ N
$F_{2y}=F_2\sin 90 = 6\cdot 1 = 6$ N
Komponen vektor $\vec{F_3}$ :
$F_{3x}=-F_3\cos 45 = -10\cdot \frac{1}{2}\sqrt{2} = -5\sqrt{2}$ N
$F_{3y}=F_3\sin 45 = 10\cdot \frac{1}{2}\sqrt{2} = 5\sqrt{2}$ N
$\Sigma F_{x}=F_{1x}+ F_{2x}+F_{3x}= 5\sqrt{2} + 0 – 5\sqrt{2} = 0$ N
$\Sigma F_{y}=F_{1y}+ F_{2y}+F_{3y}= 5\sqrt{2} + 6 + 5\sqrt{2} = (10\sqrt{2} + 6)$ N
Besar vektor resultan :
$$
\begin{align*}
\left|\vec{R} \right| &= \sqrt{(\Sigma F_x)^2+(\Sigma F_y)^2} \\
&= \sqrt{(0)^2+\left(10\sqrt{2}+6 \right)^2} \\
&= \sqrt{\left(10\sqrt{2}+6 \right)^2} \\
&= \left(10\sqrt{2}+6 \right) \quad \textrm{N}
\end{align*}
$$
Jawaban soal vektor no. 7 : D
Soal Vektor No. 8
Dua vektor gaya membentuk sudut 60o dan mempunyai resultan gaya 14 N. Jika besar vektor gaya $\vec{F_1}$= 10 N, besar vektor $\vec{F_2}$ adalah ….
A. 140 N
B. 24 N
C. 16 N
D. 6 N
E. 4 N
Pembahasan soal vektor no. 8 :
$$
\begin{align*}
R &= \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos \theta } \\
14 &= \sqrt{10^2 + F_2^2 + 2\cdot 10 \cdot F_2\cos 60 } \\
14 &=\sqrt{100 + F_2^2 + 20 \cdot F_2\cdot \frac{1}{2} } \\
14^2 &=100 + F_2^2 + 10 \cdot F_2 \\
196 -100 &= F_2^2 + 10 \cdot F_2 \\
96 &= F_2^2 + 10 \cdot F_2 \\
F_2^2 + 10 \cdot F_2 – 96 &= 0 \\
(F_2 + 16 )(F_2 – 6) &= 0 \\
F_2 – 6 &= 0 \\
F_2 &= 6 \quad \textrm{N}
\end{align*}
$$
Jawaban soal vektor no. 8 : D
Soal Vektor No. 9
Jika sebuah vektor kecepatan $\vec{v}$= 14 m/s$ diuraikan menjadi dua vektor yang saling tegak lurus dan salah satu vektor uraiannya membentuk sudut 60o dengan vektor $\vec{v}$, besar masing-masing vektor uraiannya adalah ….
A. 7 m/s dan $7\sqrt{2}$ m/s
B. 7 m/s dan $7\sqrt{3}$ m/s
C. 7 m/s dan $14\sqrt{3}$ m/s
D. 14 m/s dan $14\sqrt{2}$ m/s
E. 14 m/s dan $14\sqrt{3}$ m/s
Pembahasan soal vektor no. 9 :
vx=14cos60=7m/s
vy=14sin60= $7\sqrt{3}$ m/s
Jawaban soal vektor no. 9 : B
Soal Vektor No. 10
Perhatikan gambar berikut.
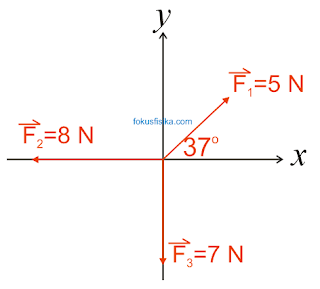
Besar resultan ketiga gaya tersebut adalah ….
A. 8 N
B. 7 N
C. 5 N
D. N
E. 4 N
Pembahasan soal vektor no. 10 :
Komponen vektor F1 :
F1x=5cos37= 4 N
F1y=5sin37= 3 N
Komponen vektor F2 :
F2x=−8 N
F2y=0 N
Komponen vektor F3 :
F3x=0 N
F3y=−7 N
ΣFx=F1x+F2x+F3x=4–8+0=−4N
ΣFy=F1y+F2y+F3y=3+0-7=−4N
Vektor resultan :
$$
\begin{align*}
\left|\vec{R} \right| &= \sqrt{(\Sigma F_x)^2+(\Sigma F_y)^2} \\
&= \sqrt{(-4)^2+(-4)^2} \\
&= \sqrt{16+16} \\
&= \sqrt{2\cdot 16} \\
&= 4\sqrt{2} \quad \textrm{N}
\end{align*}
$$
Jawaban soal vektor no. 10 : D
Pembahasan Soal UN SMA tentang Vektor.
Perhatikan gambar di bawah!
Besar resultan ketiga gaya tersebut adalah ….
A. 0 N
B. $2\sqrt{3}$ N
C. $4\sqrt{3}$ N
D. $8\sqrt{3}$ N
E. $12\sqrt{3}$ N
Pembahasan :
$F_{1x} = F_1 \cos 30 = 4\cdot \frac{1}{2}\sqrt{3} = 2\sqrt{3}$ N
$F_{1y} = F_1 \sin 30 = 4\cdot \frac{1}{2} = 2$ N
$F_{2x} = -6\sqrt{3}$ N
F2x = 0 N
F3x = 0 N
F3y = -2 N
$\Sigma F_{x}=F_{1x}+ F_{2x}+F_{3x}= 2\sqrt{3} – 6\sqrt{3} + 0 = -4\sqrt{3}$ N
$\Sigma F_{y}=F_{1y}+ F_{2y}+F_{3y}= 2 + 0 -2 = 0$ N
Besar vektor resultan :
$$
\begin{align*}
\left|\vec{R} \right| &= \sqrt{(\Sigma F_x)^2+(\Sigma F_y)^2} \\
&= \sqrt{\left(-4\sqrt{3} \right)^2+\left(0 \right)^2} \\
&= 4\sqrt{3} \quad \textrm{N}
\end{align*}
$$
Jawaban : C
Soal Vektor UN Fisika 2017
Sebuah benda mula-mula di titik A(0,0) kemudian bergerak selama 2 sekon ke titik B(4,2). Selanjutnya bergerak lagi selama 3 sekon ke titik C(8,6). Kecepatan rata-rata gerak benda adalah ….
A. 1 m.s-1
B. 1,5 m.s-1
C. 2 m.s-1
D. m.s-1
E. 4,75 m.s-1
Pembahasan Soal Vektor UN Fisika 2017 :
Perhatikan gambar perpindahan benda berikut ini:
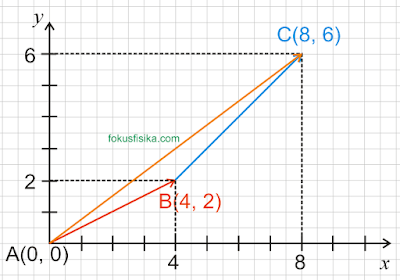
Dari gambar diketahui :
xAB = 4 m
yAB = 2 m
xBC = 4 m
yBC = 4 m
Komponen perpindahannya :
Δx = xAB + xBC = 4 + 4 = 8 m
Δy = yAB + yBC = 2 + 4 = 6 m
Besar perpindahan :
$\Delta r = \sqrt{\Delta x_2^2 + \Delta 2_2^2} = \sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10$
Waktu yang dibutuhkan : Δt = 2 + 3 = 5 s
Kecepatan rata-rata gerak benda:
$v=\frac{\Delta r}{\Delta t} = \frac{10}{5} = 2$ m.s-1
Jawaban : C
Setelah mempelajari soal dan pembahasan vektor fisika di atas, diharapkan pembaca dapat memahami materi tersebut dengan baik. Sehingga kemampuan dalam belajar fisika akan semakin meningkat. Terima kasih.