Soal 1
Setelah 2 s dari keadaan diam, kecepatan benda menjadi 4 m/s. Kemudian, benda bergerak dengan kecepatan konstan. Waktu total, dari waktu diam, yang dibutuhkan benda untuk mencapai jarak total 10 m adalah …..
A. 7,5 s
B. 6,0 s
C. 5,5 s
D. 4,5 s
D. 3,5 s
Pembahasan :
Percepatan benda selama t1 = 2 sekon pertama adalah :
\begin{aligned}
a &= \frac{v}{t} \\
&= \frac{4}{2} \\
&= 2 \quad \textrm{m/s}^2
\end{aligned}
Jarak tempuh benda saat 2 s pertama adalah :
\begin{aligned}
s &= v_o t + \frac{1}{2}at^2 \\
&= 0\cdot 2 + \frac{1}{2}\cdot 2\cdot 2^2 \\
&= 4 \quad \textrm{m}
\end{aligned}
Sisa jarak tempuh = 10 m – 4 m = 6 m
Selama 6 m, kecepatan konstan 4 m/s, sehingga membutuhkan waktu :
\begin{aligned}
t_2 &= \frac{s}{v} \\
&= \frac{6}{4} \\
&= 1,5 \quad \textrm{s}
\end{aligned}
Waktu total yang dibutuhkan benda : t = t1 + t2 = 2 + 1,5 = 3,5 s
Jawaban : E
Soal 2
Sebuah kereta mendapat percepatan 2 m/s2 selama 10 s dari keadaan diam, lalu diperlambat dengan perlambatan 4 m/s2 sampai berhenti. Jarak total yang ditempuh kereta tersebut adalah ….
A. 80 m
B. 100 m
C. 150 m
D. 200 m
E. 250 m
Pembahasan :
Jarak tempuh kereta selama dipercepatan :
\begin{aligned}
s_1 &= v_o t + \frac{1}{2}at^2 \\
&= 0\cdot 10 + \frac{1}{2}\cdot 2\cdot 10^2 \\
&= 100 \quad \textrm{m}
\end{aligned}
Kecepatan kereta selama 10 sekon pertama :
\begin{aligned}
v_1 &= a\cdot t\\
&= 2\cdot 10 \\
&= 20 \quad \textrm{m/s}
\end{aligned}
Jarak tempuh kereta selama diperlambat :
\begin{aligned}
v_t^2 &= v_1^2 – 2\cdot a \cdot s_2\\
0^2 &= 20^2 – 2\cdot 4 \cdot s_2 \\
0 &= 400 -8s_2 \\
8s_2 &= 400 \\
s_2 &= 50 \quad \textrm{m}
\end{aligned}
Jarak total kereta : stot = s1 + s2 = 100 m + 50 m = 150 m
Jawaban : C
Soal 3 ( UN 2011 )
Sebuah benda bergerak dengan lintasan seperti pada grafik berikut.
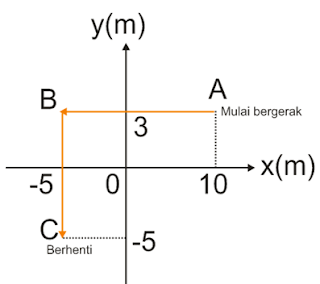
Perpindahan yang dialami benda sebesar ….
A. 23 m
B. 21 m
C. 19 m
D. 17 m
E. 15 m
Pembahasan :
AB = 15 m
BC = 8 m
Besar perpindahan benda :
\begin{aligned}
r &= \sqrt{AB^2 + BC^2}\\
&= \sqrt{15^2 + 8^2}\\
&= \sqrt{225 + 64}\\
&= \sqrt{289}\\
&= 17 \quad \textrm{m}
\end{aligned}
Jawaban : D
Soal 4
Seseorang memacu sepeda motor dari rumahnya ke arah utara sejauh 6 km, lalu berbelok ke timur sejauh 8 km. Posisi orang tersebut dari rumahnya setelah melakukan perjalanan tersebut adalah ….
A. 2 km ke arah timur
B. 14 km ke arah timur laut
C. 14 km ke arah barat daya
D. 10 km ke arah timur laut
E. 10 km ke arah barat daya
Pembahasan :
Perhatikan ilustrasi berikut :
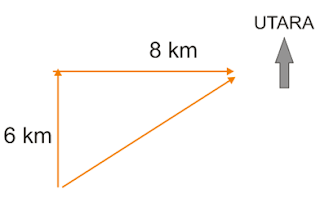
Berdasarkan ilustrasi di atas besar perpindahan sepeda motor :
\begin{aligned}
r &= \sqrt{8^2 + 6^2}\\
&= \sqrt{64 + 36}\\
&= \sqrt{100}\\
&= 10 \quad \textrm{m}
\end{aligned}
Jadi perpindahan sepeda motor sejauh 10 m ke arah timur laut.
Jawaban : D
Soal 5
Perhatikan grafik kecepatan terhadap waktu dari kereta yang bergerak menurut garis lurus dalam waktu 4 s.
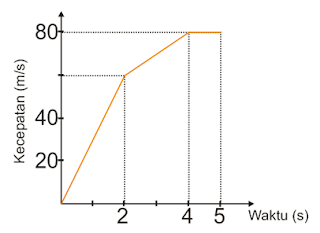
Dari grafik ini dapat ditentukan jarak yang ditempuh dalam waktu 4 s, yaitu ….
A. 260 m
B. 200 m
C. 140 m
D. 70 m
E. 60 m
Pembahasan :
Untuk t = 0 sampai t = 2 sekon, jarak yang ditempuh = luas segitiga
\begin{aligned}
s_1 &= \frac{1}{2}\cdot alas \cdot tinggi\\
&= \frac{1}{2}\cdot 2 \cdot 60\\
&= 60 \quad \textrm{m}
\end{aligned}
Untuk t = 2 sampai t = 4, jarak yang ditempuh = luas trapesium
\begin{aligned}
s_2 &= \frac{(a+b)}{2}\times t \\
&= \frac{(60+80)}{2}\times 2 \\
&= 140 \quad \textrm{m}
\end{aligned}
Total jarak yang ditempuh selama 4 s :
\begin{aligned}
s_{total}&= s_1 + s_2\\
&= 60 + 140 \\
&= 200 \quad \textrm{m}
\end{aligned}
Jawaban : B
Soal 6 ( Soal SNMPTN 2010 )
Sebuah batu kecil dilempar ke atas dan mendarat di sebuah papan yang terletak 2 m di atas titik pelemparan. Jika kecepatan awal batu dilempar ke atas adalah 7 m/s, kecepatan batu ketika mengenai sasaran adalah ….
A. 0 m/s
B. -3 m/s
C. 3 m/s
D. 3,4 m/s
E. 4 m/s
Pembahasan :
Kecepatan batu ketika mengenai sasaran dapat ditentukan dengan persamaan :
\begin{aligned}
v_t^2 &= v_o^2 – 2gh \\
&= 7^2-2\cdot 10\cdot 2 \\
&= 49 – 40 \\
&= 9 \\
v_t &= 3 \quad \textrm{m/s}
\end{aligned}
Jawaban : C
Soal 7
Dua bola dilempar vertikal ke atas pada saat yang bersamaan. Jika bola memiliki kecepatan awal masing-masing v1 = 20 m/s dan v2 = 24 m/s, tentukan jarak antara kedua bola ketika bola pertama mencapai ketinggian maksimumnya.
A. 20 m
B. 28 m
C. 16 m
D. 14 m
E. 8 m
Pembahasan :
Ketinggian maksimum bola pertama :
\begin{aligned}
h_1 &= \frac{v_1^2}{2g} \\
&= \frac{20^2}{2\cdot 10} \\
&= \frac{400}{20} \\
&= 20 \quad \textrm{m}
\end{aligned}
Waktu yang dibutuhkan benda pertama untuk mencapai ketinggian maksimum :
\begin{aligned}
v_1 &= g\cdot t \\
20 &= 10t \\
t &= 2 \quad \textrm{s}
\end{aligned}
Ketinggian yang ditempuh bola kedua ketika bola pertama mencapai ketinggian maksimum (t = 2 s) :
\begin{aligned}
h_2 &= v_2 \cdot t -\frac{1}{2} g\cdot t^2 \\
&= 24\cdot 2 – \frac{1}{2}\cdot 10 \cdot 2^2 \\
&= 28 \quad \textrm{m}
\end{aligned}
Jarak antara kedua bola ketika bola pertama mencapai ketinggian maksimumnya :
\begin{aligned}
h &= h_2 – h_1 \\
&= 28 – 20 \\
&= 8 \quad \textrm{m}
\end{aligned}
Jawaban : E







Leave a Reply